Bild oben: 3D-Animation setzt auf Dreiecke (Ausschnitt aus dem Film „Mesh – Eine Reise durch die diskrete Geometrie“ von Beau Janzen und Konrad Polthier). Credit: Janzen, Polthier
Im Studium musste ich mir anhören:
‚Wieso machst du denn Bilder?‘
Konrad Polthier ist Professor für Mathematik an der Freien Universität Berlin. Als einer der Erfinder der diskreten Differenzialgeometrie ist er sehr geschickt darin, durch Visualisierung neue Zugänge zu mathematischen Fragestellungen zu öffnen. Das kommt in Fachkreisen gut an, begeistert aber auch Laien – zum Beispiel das Publikum von Hollywood-Blockbustern, das dank Polthiers Forschung in den Genuss lebensechter 3D-Animationen kommt. In diesem und vielen weiteren Gebieten sind Mathematiker*innen mit Geometrie-Schwerpunkt gefragt.

Bild oben: Prof. Dr. Konrad Polthier, Freie Universität Berlin. Credit: Die Hoffotografen, Berlin
- Lehrerspezial: Herr Polthier, Sie beschäftigen sich mit der Visualisierung von Mathematik. Was könnten Bilder mathematisch beisteuern?
-
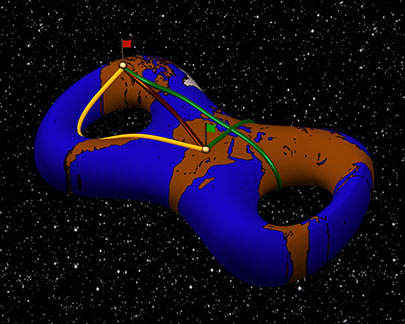
Konrad Polthier: Mathematik ist eine spannende Sache. Aber wenn man sich Mathematikbücher ansieht, versteht man erst einmal nicht viel. Selbst in der Geometrie ist es so, dass die geometrischen Formen in den Büchern oft nicht dargestellt sind. Man beweist Eigenschaften oder die Existenz bestimmter Objekte, aber wie sie aussehen, wird nicht gezeigt. Ein Beispiel: Die kürzeste Verbindung zwischen zwei Punkten in einer Ebene ist eine Gerade. Auf der Erde ist die kürzeste Verbindung ein Großkreis. Und es gibt noch viel komplexere mathematische Objekte, für die man die kürzesten Verbindungen berechnen kann – aber man bekommt sie kaum je zu sehen und es bleibt sehr abstrakt. Solche Überlegungen haben mich motiviert, ein Buch über „Bilder der Mathematik“ zu veröffentlichen. Es zeigt, welche Objekte in verschiedenen Bereichen der Mathematik behandelt werden und welche Eigenschaften sie haben.Bild rechts: Im Unterschied zu Geraden im euklidischen Raum können zwischen zwei Punkten auf einer Fläche verschiedene kürzeste Kurven (Geodätische) existieren (Ausschnitt aus dem Video „Geodesics and Waves“). Credit: Arnez, Polthier und Steffens, Teitzel
- Könnten Sie das bitte einmal an einem Beispiel erklären?
-
Zum Beispiel beschäftigt sich die Geometrie mit sogenannten Seifenhäuten. Diese entstehen, wenn man eine geschlossene Drahtkurve in eine Seifenlösung taucht und wieder herauszieht. Je nachdem, welche Form der Draht hat, entstehen sehr unterschiedliche Seifenhäute bzw. Minimalflächen. Eine der offenen Fragen ist: Gibt es noch viele andere Seifenhäute? Seit 200 Jahren beschäftigen sich Menschen aus der Geometrie, Variationsrechnung oder Topologie mit Fragen wie dieser. Aber wir haben sie zum ersten Mal sichtbar gemacht und dadurch auch neue Forschung angestoßen.


Bild oben links: Im Video „Palast der Seifenhäute“ von Beau Janzen und Konrad Polthier sind berühmte Minimalflächen zu sehen. Bild oben rechts: Die Entdeckungen von Bernhard Riemann und Celso José da Costa. Credit: Janzen, Polthier - Wie kommt es, dass Bilder in der Mathematik früher so eine geringe Rolle gespielt haben?
- Das war gar nicht immer so. Im 19. Jahrhundert war die Mathematik sehr bildlich. Deutschland war eine Hochburg, um mathematische Modelle aus Gips zu formen. 1893 wurden sie sogar auf der Weltausstellung in Chicago gezeigt. Aber durch die Anschaulichkeit wurde auch anschaulich argumentiert, und das wurde dann später zum Teil widerlegt. Also musste man die Anschaulichkeit wieder herausnehmen und mathematisch viel präziser definieren und argumentieren. Das blieb mindestens bis in die 1980er Jahre so.
- Und über Computertechnologien haben dann die Bilder wieder mehr an Bedeutung gewonnen?
- Genau. Heute haben wir ja im Internet eine regelrechte Bilderflut mit vielen tollen Visualisierungen aus der Wissenschaft. Aber zunächst wurde das nicht richtig akzeptiert. Im Studium musste ich mir anhören: „Wieso machst du denn Bilder? Mach doch lieber Theoriebeweise!“ Das habe ich auch gemacht, aber nebenbei habe ich an den Bildern gearbeitet und bin mit der Zeit auf mehr Akzeptanz gestoßen. Damals kamen auch die ersten Forschungsprojekte auf, die nach mathematischen Techniken suchten, um solche Bilder überhaupt zu entwickeln. Viele dieser Methoden sind dann in die Computergrafik eingeflossen.
- Nach den Bildern haben Sie auch Filme produziert. Wie kam es dazu?
-
In den 1990er Jahren habe ich angefangen, kurze Filme zu produzieren, zum Beispiel zu Seifenhäuten und ihren mathematischen Eigenschaften. Dadurch bin ich in Kontakt mit Mathematiker*innen und Mathematik-Interessierten weltweit gekommen, die ähnliche Filme gemacht haben. Darunter war auch Beau Janzen, ein Computergrafiker aus Los Angeles, der damals schon bei Hollywood-Produktionen mitarbeitete. Ich lud ihn nach Berlin ein und hier haben wir dann unter anderem gemeinsam den Film „Mesh – Eine Reise durch die diskrete Geometrie“ produziert. Über diese Verbindung ist es auch dazu gekommen, dass wir die Mathematik entwickelt haben, die in Hollywoodfilmen bei 3D-Animationen zum Einsatz kommt, die sogenannte diskrete Differenzialgeometrie.Bild rechts: Der Ikosaeder, einer der vier Platonischen Körper
(Ausschnitt aus dem Film „Mesh – Eine Reise durch die diskrete Geometrie“ von Beau Janzen und Konrad Polthier). Credit: Janzen, Polthier - Wie kann man sich das vorstellen?
- Die Computermodelle sind aus Dreiecksnetzen aufgebaut. Wenn Sie zum Beispiel einen Crashtest mit einem Auto simulieren möchten, stellen Sie das Auto als Netz aus Dreiecken dar. Bei dem Crash verformt sich das Auto, dadurch verändern sich die Eckpunkte der Dreiecke. Aber es bleiben Dreiecke. In den 1950er Jahren hat man so etwas mit Splines gemacht – Funktionen, die aus Polynomen zusammengesetzt sind und sich mithilfe von Kontrollpunkten verformen lassen. Aber für 3D-Animationen bräuchte man sehr viele Kontrollpunkte. Deshalb ist es einfacher, mit Dreiecksnetzen zu arbeiten. Vor allem spart es Daten und Rechenzeit, das ist bei Filmen ein großer Vorteil. Die Technologie kommt aber auch in anderen Kontexten zum Einsatz, zum Beispiel in der Architektur.
- Ist die Mathematik für Computeranimationen jetzt fertig entwickelt oder gibt es noch weiteren Forschungsbedarf?
- Es war nie das Ziel, dass Monster computeranimiert laufen lernen. Das mathematische Ziel ist immer, mehr zu verstehen. Beim Film stehen im Moment eher technologische Fragen im Vordergrund. Aber in anderen Bereichen gibt es noch viel Forschungsbedarf, bei dem Visualisierungen helfen können. Wenn Sie zum Beispiel in die Natur schauen, dann scheinen viele Objekte auf den ersten Blick geometrisch sehr einfach zu sein. Einen Baumstamm können Sie als Zylinder darstellen, auch Zweige und Blätter sind kein Problem. Aber wenn Sie weiter heranzoomen, sehen sie, dass die Baumrinde in Wirklichkeit nicht glatt ist, sondern eher wie ein kleines Gebirge aussieht. Gehen Sie noch näher heran, erkennen Sie Risse, kleine Löcher – eine Vielzahl geometrischer Formen, die sehr filigran sind, nahezu fraktal. Um solch eine Detailtiefe zu modellieren, brauchen Sie eine riesige Anzahl von Dreiecken, das lässt sich derzeit noch nicht darstellen.
- Wofür sind solche Darstellungen wichtig?
- Zum Beispiel könnten Sie auf diese Weise untersuchen, wie atmungsaktiv so eine Baumrinde ist. Oder nehmen Sie an, Sie könnten die menschliche Haut so detailliert darstellen. Das könnte dazu beitragen, Alterungsprozesse besser zu verstehen. Wenn wir solche Fragen beantworten wollen, müssen wir bis auf die Molekülebene schauen. Dabei ist Visualisierung sehr hilfreich.
- In welchen Bereichen kommen Studierende unter, wenn sie sich in Mathematik auf Geometrie spezialisiert haben?
- Viele gehen in den Bereich CAD (computer-aided design), andere in die Architektur und immer mehr beschäftigen sich nach dem Studium mit Computeranimation. Es entstehen aber auch immer wieder neue Einsatzfelder. Zum Beispiel sind zuletzt einige nach dem Studium bei einem Internethandel untergekommen und entwickeln Technologien, mit denen die Käufer*innen per Körper-sScan sicherstellen können, dass sie Kleidung in der passenden Größe bestellen. Viele Studierende gründen auch eigene Unternehmen, es gibt viele verschiedene Möglichkeiten.
Zurück zum Spezial