Themenspezial
Ob Kriegslist oder Liebesbrief - geheime Botschaften
wecken Neugier. Wenn ein Absender sicherstellen
möchte, dass nur der rechtmäßige Empfänger seine
Nachricht versteht, so kann er diese verschlüsseln.
Seit der Antike hat es unzählige Versuche gegeben,
dafür sichere Methoden zu entwickeln, doch fast alle
wurden irgendwann aufgedeckt. Im Wettlauf zwischen
den Entwicklern neuer Verfahren und jenen, die sie
entschlüsseln, sind die Erstgenannten oft nur eine
Nasenlänge voraus.
Verschlüsselungsverfahren nutzen Methoden der Mathematik und
der Informatik. Längst ist daraus eine eigene Wissenschaft ent-
standen, die Kryptologie, nach dem griechischen Wort „kryptos“
für geheim. Es verwundert kaum, dass diese „Wissenschaft des
Geheimen“ auch Laien fasziniert. Dafür spricht eine Vielzahl an
populären Filmen wie etwa Dan Browns Bestseller
„The Da Vinci Code - Sakrileg“. Historisch korrekt erzählt „Enigma - das Geheimnis“ die Geschichte der Entschlüsselung der Wehrmachts-Chiffriermaschine. Der mit vier Oscars ausgezeichnete Film „A Beautiful Mind - Genie und Wahnsinn“ zeichnet die Lebensgeschichte des Mathematik-Nobelpreisträgers John Nash nach.
Diese Popularisierung der Kryptologie geht Hand in Hand mit ihrer zunehmenden Verbreitung im Alltag. Während das Thema früher vor allem für das Militär eine Rolle spielte, steigt der Bedarf in der Informationsgesellschaft: Information ist zur Handelsware geworden, und die Kryptologie bietet ihr Geleitschutz. Das gilt nicht nur für den besonders sensiblen Finanzbereich, sondern für jede digitale Kommunikation, vom einfachen Handy-Telefonat bis zum Einkauf im Internet. Die dabei eingesetzten Verschlüsselungsverfahren sind komplex und nur IT-gestützt zu bewältigen. Die grundlegenden Verschlüsselungsprinzipien selbst sind jedoch häufig verblüffend einfach und haben sich im Laufe der Geschichte nur wenig verändert.
Einige kryptologische Methoden können deshalb im Unterricht schon ab der Sekundarstufe 1 demonstriert werden:
wecken Neugier. Wenn ein Absender sicherstellen
möchte, dass nur der rechtmäßige Empfänger seine
Nachricht versteht, so kann er diese verschlüsseln.
Seit der Antike hat es unzählige Versuche gegeben,
dafür sichere Methoden zu entwickeln, doch fast alle
wurden irgendwann aufgedeckt. Im Wettlauf zwischen
den Entwicklern neuer Verfahren und jenen, die sie
entschlüsseln, sind die Erstgenannten oft nur eine
Nasenlänge voraus.
Verschlüsselungsverfahren nutzen Methoden der Mathematik und
der Informatik. Längst ist daraus eine eigene Wissenschaft ent-
standen, die Kryptologie, nach dem griechischen Wort „kryptos“
für geheim. Es verwundert kaum, dass diese „Wissenschaft des
Geheimen“ auch Laien fasziniert. Dafür spricht eine Vielzahl an
populären Filmen wie etwa Dan Browns Bestseller
„The Da Vinci Code - Sakrileg“. Historisch korrekt erzählt „Enigma - das Geheimnis“ die Geschichte der Entschlüsselung der Wehrmachts-Chiffriermaschine. Der mit vier Oscars ausgezeichnete Film „A Beautiful Mind - Genie und Wahnsinn“ zeichnet die Lebensgeschichte des Mathematik-Nobelpreisträgers John Nash nach.
Diese Popularisierung der Kryptologie geht Hand in Hand mit ihrer zunehmenden Verbreitung im Alltag. Während das Thema früher vor allem für das Militär eine Rolle spielte, steigt der Bedarf in der Informationsgesellschaft: Information ist zur Handelsware geworden, und die Kryptologie bietet ihr Geleitschutz. Das gilt nicht nur für den besonders sensiblen Finanzbereich, sondern für jede digitale Kommunikation, vom einfachen Handy-Telefonat bis zum Einkauf im Internet. Die dabei eingesetzten Verschlüsselungsverfahren sind komplex und nur IT-gestützt zu bewältigen. Die grundlegenden Verschlüsselungsprinzipien selbst sind jedoch häufig verblüffend einfach und haben sich im Laufe der Geschichte nur wenig verändert.
Einige kryptologische Methoden können deshalb im Unterricht schon ab der Sekundarstufe 1 demonstriert werden:

Historische Geheimbotschafen
Skytale
Bereits vor über 2.500 Jahren verwendeten die Spartaner
ein militärisches Verschlüsselungsverfahren, das heute unter dem
Namen Skytale bekannt ist. Hierfür wurde ein Pergamentstreifen
um einen Stab gewickelt. Nachdem die Botschaft auf das Band
geschrieben wurde, wickelte man es wieder ab und überbrachte
es dem Empfänger. Der Stab verblieb beim Absender. Die
Botschaft konnte nur von einer Person gelesen werden, die einen
Stab mit gleichem Umfang besaß. Gelangte die Botschaft in die
Hände einer anderen Person, konnte sie die Nachricht nicht
lesen, da die Buchstaben scheinbar willkürlich auf dem Perga-
mentstreifen angeordnet waren.
Der 100 v. Chr. geborene römische Feldherr Gaius Julius Caesar ist Namensgeber einer einfachen Verschlüsselungsmethode, die sich Caesarchiffre nennt. Caesar benutzte für seine militärische Korrespondenz eine Verschiebung des Alphabets um drei Buchstaben, so dass die einzelnen Vokale und Konsonanten einer Botschaft durch die Buchstaben ersetzt wurden, die im Alphabet drei Stellen später folgten. Bei dieser Methode wird beispielsweise aus dem A ein D und aus dem B ein E. Mit Caesarchiffre verschlüsselt, liest sich das Wort „Mathematikunterricht“ so: „Pdwkhpdwlnxqwhuulfkw“.
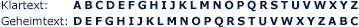
Ein einfacher Caesar-Schlüssel lässt sich mit zwei verschieden großen, runden Scheiben bauen, auf deren Rändern das Alphabet aufgetragen wird. Zunächst legt man sie so übereinander, dass sich gleiche Buchstaben gegenüberstehen. Dreht man die Scheiben gegeneinander, so steht beispielsweise das „A“ einer Scheibe über dem „D“ der anderen. So lassen sich die Buchstaben der verschlüsselten Nachricht leicht ablesen.
Weil die Caesarchiffre auf der Verschiebung eines einzigen Alphabets beruht, zählt man sie zu den so genannten monoalphabetischen Verschlüsselungsmethoden. Diese lassen sich relativ leicht dechiffrieren, indem man sich nach der Häufigkeit von Vokalen oder Konsonanten richtet. Immer wieder vorkommende Zeichen stehen wahrscheinlich für häufige Vokale wie e oder a.

Enigma
Die Enigma (griechisch „Rätsel“) ist eine der bekanntesten Chif-
friermaschinen der Geschichte. Sie wurde von der deutschen Wehrmacht im Zweiten Weltkrieg eingesetzt und beruht auf dem Prinzip der polyalphabetischen Verschlüsselung. Äußerlich ähnelt die Enigma einer Schreibmaschine. Sie besteht aus einer Tastatur, einem Satz von drei austauschbaren Walzen und einem Lampenfeld zur Anzeige. Durch die Walzen werden je nach ihrer Position elektrische Kontakte hergestellt, die im Anzeigenfeld einen bestimmten Buchstaben aufleuchten lassen. Die Walzen drehen sich nach jedem Tastendruck. Jeder Buchstabe wird also anders verschlüsselt („polyalphabetisch“).
Wie komplex die vielfache Verschlüsselung ist, zeigt die Geschichte der Enigma: Obwohl das erste Modell bereits im Jahr 1918 gebaut wurde, konnte die Methode erst 1943 vollständig aufgedeckt werden. Wissenschaftler aus Großbritannien, Polen, Frankreich und den USA arbeiteten dafür unter dem Decknamen „Ultra“ zusammen. Sie benötigten Rechenmaschinen, die bis zu zwei Meter hoch und fünf Meter breit waren. Die Entschlüsselung der Botschaften trug wesentlich zum Sieg der Alliierten über das Deutsche Reich bei. Die Enigma kann heute noch im Deutschen Museum in München oder im Museum für Kommunikation in Berlin besichtigt werden.
Kryptologie und moderne Technologie
Zwei grundlegende Prinzipien
Beim Security by Obscurity-Prinzip dagegen bleibt die Verschlüsselungsmethode unbekannt. Wie ein Haustürschlüssel unter dem Blumentopf: Jeder könnte ihn benutzen, wenn er wüsste, wo er sich befindet. In der Praxis werden häufig beide Prinzipien miteinander verbunden. Sowohl der Schlüssel als auch die Verschlüsselungsmethode bleiben unbekannt.
Symmetrische und asymmetrische Verschlüsselung
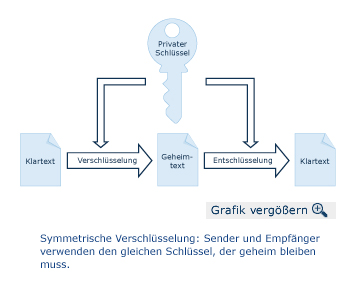
Symmetrische Verschlüsselung
Symmetrische Verschlüsselungsverfahren wie die Caesarchiffre und die Enigma, aber auch moderne Block-
chiffren wie DES setzen voraus, dass Absender und Empfänger den gleichen Schlüssel verwenden. Wird dieser Schlüssel bekannt, ist keine Datensicherheit mehr gegeben. Deshalb können sich Sender und Empfänger nicht öffentlich über den Schlüssel verständigen.
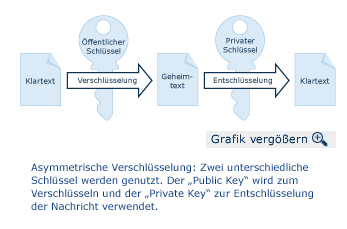
Asymmetrische Verschlüsselung: Die RSA-Methode
In den 1970er Jahren entwickelten Ronald L. Rivest, Adi Shamir und Leonard Adleman am amerikanischen MIT die nach ihren Initialen benannte RSA-Methode. Sie wird auch Public-Key-Verschlüsselung genannt, weil sie mit einem öffentlich einsehbaren Schlüssel arbeitet. Sie zählt zu den asymmetrischen Verfahren, weil Sender und Empfänger zwei unterschiedliche Schlüssel verwen-
den. Der Schlüssel, der zum Kodieren verwendet wird, ist nicht dazu geeignet, die Botschaft zu dechiffrieren - ähnlich einem Schlüssel, mit dem man eine Tür zwar verschließen, aber nicht öffnen kann. Der Kodierschlüs-
sel heißt auch „Public Key“. Nur mit dem zweiten Schlüssel, dem „Private Key“, den allein der Empfänger kennt, kann die Nachricht wieder in Klartext umgewan-
delt werden. Die RSA-Methode widerlegte die bis dato unter Mathematikern weit verbreitete Ansicht, dass ein Public-Key-Verfahren prinzipiell unmöglich sei.
Ablauf einer Public-Key-Verschlüsselung (s. Schaubild):
| 1. | Der Empfänger (A) möchte vom Absender (B) eine kodierte Botschaft erhalten. |
| 2. | A entwickelt anhand eines Rechenverfahrens zwei Schlüssel: einen „öffentlichen“ und einen „geheimen“. |
| 3. | A übermittelt B den öffentlichen Schlüssel. |
| 4. | B chiffriert seine Botschaft mit dem öffentlichen Schlüssel und übermittelt sie an A. Andere Personen kennen möglicherweise den öffentlichen Schlüssel, können die Botschaft aber trotzdem nicht entschlüsseln. |
| 5. | A dechiffriert die Nachricht mit dem privaten Schlüssel. |
Bei der asymmetrischen Verschlüsselung können sich Sender und Empfänger öffentlich über den Schlüssel austauschen. Nach diesem Prinzip funktioniert zum Beispiel das im Internet verbreitete https-Protokoll: Obwohl jede Internetverbindung von Dritten belauscht werden kann, bleibt die Verschlüsselung sicher, solange der Private Key nicht übermittelt wird. Die RSA-Methode hat jedoch einen Nachteil: Computer benötigen deutlich mehr Rechenzeit, um sie anzuwenden. In modernen Computersystemen wird daher meist eine Mischung aus symmetrischen und asymmetrischen Verfahren angewendet. Mit der RSA-Methode wird der Schlüssel auf sichere Weise ausgetauscht. Anschließend kommt er in einem symmetrischen Verfahren zur Anwendung.
Der Rechenweg der RSA-Verschlüsselung ist relativ einfach. Mit kleineren Zahlen können bereits Schüler der Sekundarstufe 1 eigene Schlüssel generieren und einander verschlüsselte Botschaften schicken.
Vorschlag zur Unterrichtsgestaltung
Rechenweg zur Entwicklung eines RSA-Schlüssels in der Sekundarstufe 1
